JFRMCブログ
レーシングマシンについての記事は「その他」にもあります。
シルバーストーンサーキットの飛行場
シルバーストーンが飛行場に造られたサーキットということがよく知られています。シルバーストン・サーキット - Wikipedia
これは1983年イギリスGPの映像に写る飛行機。
手前のG-BJYBはセスナ441で、その陰のG-ATDAはパイパーPA-28-160 チェロキーのようです。
現在のシルバーストーンは改修により飛行場としての役割は終えたようです。
PR
住友電気工業のディスクブレーキ
住友電気工業のディスクブレーキ事業は、子会社の住友電工ブレーキシステムズに移管され、現在はアイシングループのアドヴィクスに受け継がれています。
車関係で「住友」といえば住友ゴム(ダンロップ)もよく知られています。また、イギリスのダンロップといえばディスクブレーキを供給していたことが知られています。1964年に登場したホンダのRA271もダンロップのディスクブレーキだったという記憶です。
ですから、住友電気工業のディスクブレーキはダンロップのディスクブレーキの技術導入で始まったのではないかと想像していました。
で、「住友電工の歴史」(住友電気工業1977)、「住友電工百年史」(1999住友電気工業)では、
1959 日本ダンロップ護謨が住友電気工業に資本参加要請(1960 日本ダンロップ護謨に住友電気工業、住友商事が資本参加、1963 日本側の出資比率が50%を超え、社名が住友ゴム工業株式会社に)
↓
1959 住友電気工業社長が英ダンロップ訪問
↓
1959.12 日本ダンロップ護謨を通じて英ダンロップから「英ダンロップは日本でディスクブレーキのライセンスを出す場合、住友に優先権を認めたい」と申し出
↓
1961初頭 住友電気工業がブレーキ事業進出を決断
↓
1962 住友電気工業の技術者が英ダンロップで実習
↓
1963.1 同社にブレーキ部発足(9月にブレーキ事業部に)
↓
1963.3 同社と英ダンロップがディスクブレーキ製造技術について技術提携
↓
1963.6 同社がディスクブレーキ製造開始
↓
1964.1 同社伊丹製作所に専用トランスファーマシン設置
ということでした。
その後、英ダンロップがディスクブレーキ部門をガーリングに譲渡したため、住友電工はさらに苦労することになります。
二輪車用は1971年のヤマハ向け納入が始まります。
自衛隊の階級名の見直し、木原官房長官「スピード感持って検討」
自衛隊の階級名の見直し、木原官房長官「スピード感持って検討」
「自衛隊の階級は、自衛隊法で最高位の「将」以下、16階級ある。「大将」「大佐」などを使う海外とは異なり、「将」「1佐」などの呼称を使ってきた。自衛隊の軍事色を薄めるためだが、自民党と日本維新の会は連立合意書で「現在の自衛隊の階級の国際標準化を2026年度中に実行する」と明記した。」
旧軍の階級の大佐(自衛隊は1佐)は
アメリカ陸軍、空軍、海兵隊 Colonel
アメリカ海軍 Captain
イギリス陸軍、海兵隊 Colonel
イギリス空軍 Group Captain
イギリス海軍 Captain
ドイツ陸軍、空軍 Oberst
ドイツ海軍 Kapitän zur See
に相当します。
階級名は国によって違いますし、各国軍内部ですら統一されていません。
1佐を大佐に改めるのは、国際標準化ではなく旧軍化です。
海外の階級名を訳する時に、旧軍式の大佐と訳するから自衛隊の階級との対比ができないだけで、1佐と訳せばいいだけのことです。
階級名を変更することの是非はここでは議論しませんが、「階級の国際標準化」は理由になっていません。自民党、維新の会は、自衛隊の1佐が海外では国、軍を問わずTaisaだと思っているのでしょう。
旧軍の階級の大佐(自衛隊は1佐)は
アメリカ陸軍、空軍、海兵隊 Colonel
アメリカ海軍 Captain
イギリス陸軍、海兵隊 Colonel
イギリス空軍 Group Captain
イギリス海軍 Captain
ドイツ陸軍、空軍 Oberst
ドイツ海軍 Kapitän zur See
に相当します。
階級名は国によって違いますし、各国軍内部ですら統一されていません。
1佐を大佐に改めるのは、国際標準化ではなく旧軍化です。
海外の階級名を訳する時に、旧軍式の大佐と訳するから自衛隊の階級との対比ができないだけで、1佐と訳せばいいだけのことです。
階級名を変更することの是非はここでは議論しませんが、「階級の国際標準化」は理由になっていません。自民党、維新の会は、自衛隊の1佐が海外では国、軍を問わずTaisaだと思っているのでしょう。
テクニカルコース(8)
テクニカルコース に、鈴鹿サーキットの航空写真に直線長(推定)、コーナー半径(公式)を記入したものを載せていましたが、平忠彦(1986年型YZR500(0W81))のシフト地点(平忠彦写真集 きらめく汗のむこうに(角川書店1987)を参考)を加筆しました。
これです。
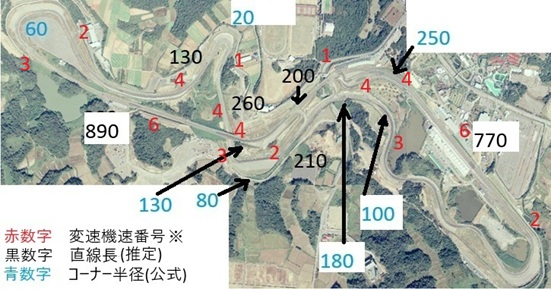
これです。
テクニカルコース(7)
これまでの記事に加筆してまとめました。
テクニカルコース
例えば、下の赤文字が追加分です。
・・・・・・・・・・・・・・・・・・・・・
テクニカルコース
例えば、下の赤文字が追加分です。
・・・・・・・・・・・・・・・・・・・・・
これらの関係から、700m加速するのに要する時間を計算する。さらに、コーナー脱出速度を10%上げた時も同様に加速時間を計算した。
低速コーナー
脱出速度80km/h 11.56秒
脱出速度88km/h 11.47秒(0.09秒短縮) 出力向上3PS相当
高速コーナー
脱出速度200km/h 9.90秒
脱出速度220km/h 9.59秒(0.31秒短縮) 出力向上17PS相当
高速コーナーの方がコーナー脱出速度を1割上昇させた効果が大きいことがわかる。 200km/hの1割上昇ではなく、80km/hと同じ8km/h上昇で計算してみても
脱出速度208km/h 9.78秒(0.12秒短縮) 出力向上7PS相当
となり、脱出速度上昇による直線加速時間短縮効果が低速コーナーより大きい。
カレンダー
リンク
カテゴリー
フリーエリア
最新CM
最新記事
(01/31)
(01/30)
(01/29)
(01/27)
(01/26)
最新TB
プロフィール
HN:
野田健一
性別:
男性
